Make Your Own Physics Simulations
You might not know it, but you already have everything you need in order to write simulations. Namely the browser that you are viewing this webpage with, and a text editor - which are included with every operating system. If you are unfamiliar with use of a text editor and have never written computer code before, then you should look at the introductory article here. We'll start with a simple simulation of a projectile's motion.
Setting up the simulation loop
The code below is the basic skeleton used in this article. You can copy and paste it into a text editor, and then save as a .html file. Note, if you double click on a code panel, then it will hide the row numbers and make it easier to copy.
<html>
<body>
<canvas id="myCanvas"></canvas>
</body>
<script>
// Graphics context
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d");
// Simulation variables
var fps = 32;
// Update function
function update(){
}
// Start simulation
var intervalId = setInterval(update, 1000 / fps);
</script>
</html>
Remember that we're only interested in what is happening between <script> and </script>. We start by creating thectx variable that will allow us to draw on the canvas. We then define a function called update, and use setInterval to call it a certain number of times per second (fps).
What we're actually doing is telling the browser how long to wait between calling the update function, but the result is pretty much the same. If we're aiming for 10 frames per second, then the browser will try to call the update function every 1000 / 10 = 100 milliseconds. If you're unfamiliar with a function, then it is just a chunk of code that has been divided off from the rest so that we can run it when we want to.
Drawing Something
If you open the webpage that you've just created, then you aren't going to see anything. It will probably be running away quite happily at 32 frames per second, but it isn't doing anything else. Lets change that by adding a projectile.
Underneath the simulation variables (but above the function) add:
// Projectile variables var x = 0; var y = 20;
Modify the update function to be:
// Update functionfunction update(){ x++; // move to right // Draw a circle ctx.beginPath(); ctx.arc(x, y, 4, 0, 2 * Math.PI, false); ctx.fillStyle = '#DD0000'; ctx.fill(); }
Now if you save the file and refresh the webpage, you should see a red line drift across from the left to the right.
All we've done is create two variables (x and y) to store the location of our projectile. Each time the update function is called (probably still 32 times per second), we add 1 to the x value (x++), and then draw a circle at that location. Because we never clear the screen, the line that you see is all the old circles that were drawn in previous updates. Using ++ is a short-hand for incrementing, or adding 1, to a variable.
Projectile angle
A horizontal line is pretty dull. You want to be firing projectiles at different angles and different velocities. That's what we'll look at next.
The first thing to note is that we can consider the vertical and horizontal motion of the projectile separately. If you could throw a ball straight up in the air with exactly the same force each time, then it would always take the same amount of time to fall back down and hit you on the head. If on one of those occasions a gust of wind came from the side, then the ball would move sideways and miss your head, but it would still reach the level of your head at the same time (ignoring the complex maths of a spinning ball).
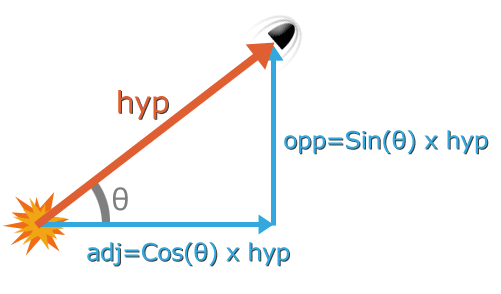
All forces acting on the projectile have a direction. Gravity for example, pulls things straight down. But even if the force acts on our projectile from an angle, we can separate it into vertical and horizontal components using trigonometry, and then deal with them separately.
Update the projectile variables so that you can provide a velocity (v) and angle (a), and then have the browser work out the x and y velocities:
// Projectile variables var x = 0; var y = 20; var v = 3; var a = 45 * Math.PI / 180; var vx = Math.cos(a) * v; var vy = Math.sin(a) * v;
You can supply the angle in degrees (e.g. 45 in the code above), and then convert it to radians by multiplying it by pi/180.
Modify the update function again so that it uses our x and y velocities:
// Update function
function update(){
x+=vx; // move to right
y+=vy; // move down
// Draw a circle
ctx.beginPath();
ctx.arc(x, y, 4, 0, 2 * Math.PI, false);
ctx.fillStyle = '#DD0000';
ctx.fill();
}
Try using different velocities and angles, and observe the results. It will be 'upside down' at this point, but we'll fix that later.
Debugging
It can be difficult to work out what is happening just by looking at the end result. What if nothing is displayed? How can we work out what went wrong? The process of removing problems (or 'bugs') from our code is known as debugging.If you spend any time writing code, particularly if you are learning or trying something new, then you will spend a lot of time debugging.
One of the debugging tools available in browsers is the ability to display the value of a variable. Add the following code directly underneath the line: var vy = Math.sin(a) * v;
console.log("VX: " + vx);
console.log("VY: " + vy);
If you just use console.log(variableName), then you will just get the variable's value. If you use console.log("Some text" + variableName), then you will also get some text that will help identify the variable.
To see the values you will need to open the console. This is different for each browser:
- Firefox: Ctrl + Shift + K
- Chrome: Ctrl + Shift + J
- Safari: Ctrl + Alt + C
- Internet Explorer: F12, then click on the script tab? (or just use another browser).
Now when you refresh the webpage, you should see the values for vx and vy displayed.
Equations of motion
If something is only acted upon by a constant force (e.g. gravity), then it behaves in a very predictable way. So predictable in-fact that there are some very simple equations, known as the equations of motion. In this case we want to work out how far the projectile has moved, and so we'll use the equation:

Where: s is the displacement (distance moved); u is the starting velocity; t is time; a is acceleration.
We'll make things easy for ourselves, and assume that once the projectile is moving, the only force acting on it is gravity. So for the vertical motion we can replace a (acceleration) with g (gravity), so the equation becomes:

Because gravity only acts downwards, the equation for the horizontal motion is even easier. Acceleration horizontally is going to be zero, so a large chunk of the equation works out to be zero as well:

Real-time graph drawing
Now that we have our equations of motion, we can simulate an actual trajectory.
Add gravity and cycle in the area for simulation variables:
// Simulation variablesvar fps = 32;
var gravity = -9.81;
var cycle = 0;
The main change is in the update function:
// Update function
function update(){
cycle++;
var t = cycle / fps;
x = vx * t;
y = (vy * t) + (0.5 * gravity * (t*t));
// Draw a circle
ctx.beginPath();
ctx.arc(x, y, 4, 0, 2 * Math.PI, false);
ctx.fillStyle = '#DD0000';
ctx.fill();
}
The equations for calculating the x and y position are pretty much the same as described in the equations of motion section. The bit that might not be obvious is the calculation of t (time). cycle counts the number of times the update function has been called. If you divide that by how many calls there will be per second (fps), then you'll get the number of seconds that have passed.
However, if you save the file and refresh the browser, then you'll just see a red dot in the corner. Now that we're using the equations of motion, we're using actual units. The 500x400 canvas now means an area 500m x 400m. The velocity of 3 now means 3 metres per second. It barely leaves the ground. Crank the velocity (v) up to 60, and try again.
Frame-by-frame simulation
The equations give you an accurate simulation, but some computer games and simulations take a slightly different approach. Each cycle you just use the forces that are currently acting on the projectile to update the velocities. The velocities are then used to update the position.
All it takes is a slight change to the update function:
// Update function
function update(){
vy = vy + ( gravity*(1/fps) );
x += vx * (1/fps);
y += vy * (1/fps);
// Draw a circle
ctx.beginPath();
ctx.arc(x, y, 4, 0, 2 * Math.PI, false);
ctx.fillStyle = '#DD0000';
ctx.fill();
}
In this case only the y velocity is updated because that's the only one affected by gravity. Everything gets divided by fps because the velocities and acceleration are acting per second, and each cycle is only simulating a fraction of a second.
Improving the appearance
Although we have some accuracy, it's fair to say that it doesn't look quite right. Now we'll add some ground, and switch the arc the correct way up.
Add the following to the simulation variables:
var groundLevel = 370;
Where the circle is being drawn, update the y value for the arc:
ctx.arc(x, (groundLevel-y), 4, 0, 2 * Math.PI, false);
Underneath where the circle is drawn, add the code to draw the ground:
ctx.fillStyle="#00CC00"; ctx.fillRect(0,groundLevel,500,400);
Stopping the simulation
At the moment the simulation never stops - the projectile just disappears behind the ground and then off screen. We can fix that by checking when the projectile's y value is below zero. Why zero, and not ground level? The groundLevel variable is only used for drawing.
if (y < 0) {
clearInterval(intervalId);
}
Summary
Hopefully you've gained an understanding of how to create simple physics simulations, using nothing more than a text editor and a web browser. However, there's plenty of room for improvement. At the moment the fps value is just an ideal. If the simulation starts to run slowly (for example if there is lots of drawing), then the fps won't be accurate and any calculations based on it will be equally inaccurate.
This post on game development provides a solution to the fps problem, as well as a better way of setting up the simulation using objects. Also, JavaScript includes some functionality for working with time, so you can do things like find out how many milliseconds have actually passed since your last update.Whether it's better to use the equations or the frame-by-frame approach is a question that I can't answer. The equations are going to be more accurate, but the frame-by-frame option is easier to work with in a dynamic system.
Thanks to Adam Bostock and Sam O'Neil for their assistance on this article.